1. rnormalについて
今回はstataを用いて正規分布に従う変数をどのように出力し、グラフ化するかについて解説します。まず、stataを起動させたら、図１にあるように
【図1】
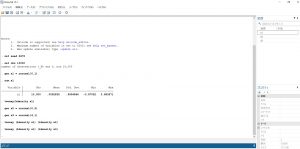
set seed 5678
set obs 10000
gen x1 = rnormal (0, 1)
とコマンドしましょう。seed 5678は「乱数を出力する元となる値を5678にしたこと」を意味しています。また、seedに続く値は任意の自然数となります。さらに、2行目で観測データ数を10000に指定して、3行目でx1を標準正規分布に従う変数と定義しています。
rnormal (a ,b)は平均a、標準偏差bの正規分布に従う数を出力するためのコマンドです。特に平均０、標準偏差１の正規分布のことを標準正規分布といいます。
このときデータエディタ（編集）を開くと図2のようになります。ⅹ1として定義された列に乱数が10000個並んでいるのが分かりますね。
【図2】
続けて
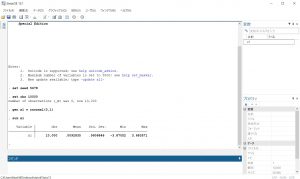
sum x1
と打ち込んでいくと、図３のような結果が出力されます。この結果を見るとMean（平均）はほぼ０、Std. Dev.（標準偏差）は1にかなり近い値になっていますね。今回はサンプル数を10000にしましたが、さらに数を増やすとMean、Std. Dev.はそれぞれ限りなく0、１に近づいていきます。このことは中心極限定理によって調べることがっできます。
【図3】
2．グラフのプロット
今回は正規分布に従う乱数を出力しましたが、その確率分布は一体どれほど正規分布に近いのかグラフを用いて直観的に理解していきましょう。
まず、前述のsum x1のあとに
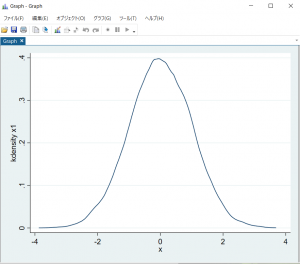
twoway (kdensity x1)
と打ち込んでみると図４のようになります。おおよそ標準正規分布に従うグラフになりましたね。これはカーネル密度推定という手法で、今回は正規分布に従う乱数を想定しましたが、それが本当に正規分布のような確率分布になるのかをグラフから直観的に理解することができます。
【図4】
次に、平均と分散の異なる正規分布をプロットするとどうなるのか、確かめてみましょう。前述のコマンドのあとに図５のように
【図5】
gen x2 = rnormal (0, 5)
gen x3 = rnormal (3, 1)
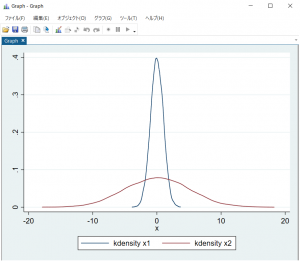
twoway (kdensity x1) (kdensity x2）
twoway (kdensity x1) (kdensity x3)
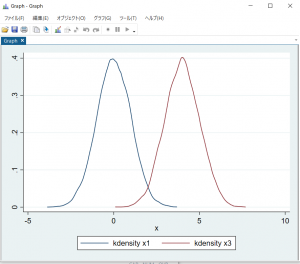
と打ち込んでグラフをプロットすると、図６，7のようになります。図６ではx2は平均がx1と同じですが分散が大きく、x1のグラフ比べて横に裾野が広くなっているのが分かりますね。一方で、図７ではx3は平均はx1と異なります、分散は等しく、x1のグラフを横にスライドさせたようなグラフになりましたね。
【図6】
【図7】
