3章 – 演習と応用4
コンテンツ
表示
a. 機会費用
労働者1人あたり、1年で
- 自動車 2台 または 小麦 30ブッシェル
なので「2台 ↔ 30ブッシェル」の関係である。
- 自動車1台の機会費用
2台作る代わりに30ブッシェル作れる ⇒ 1台あたり
\[
30/2 = 15
\] → 自動車1台=小麦15ブッシェルである。 - 小麦1ブッシェルの機会費用
30ブッシェル作る代わりに2台作れる ⇒ 1ブッシェルあたり
\[
2/30 = 1/15
\] → 小麦1ブッシェル=自動車1/15台である。 - 関係の説明
2財の機会費用は互いに逆数で、ここでは生産性が一定なので機会費用も一定(PPFが直線、傾き一定)になるのである。
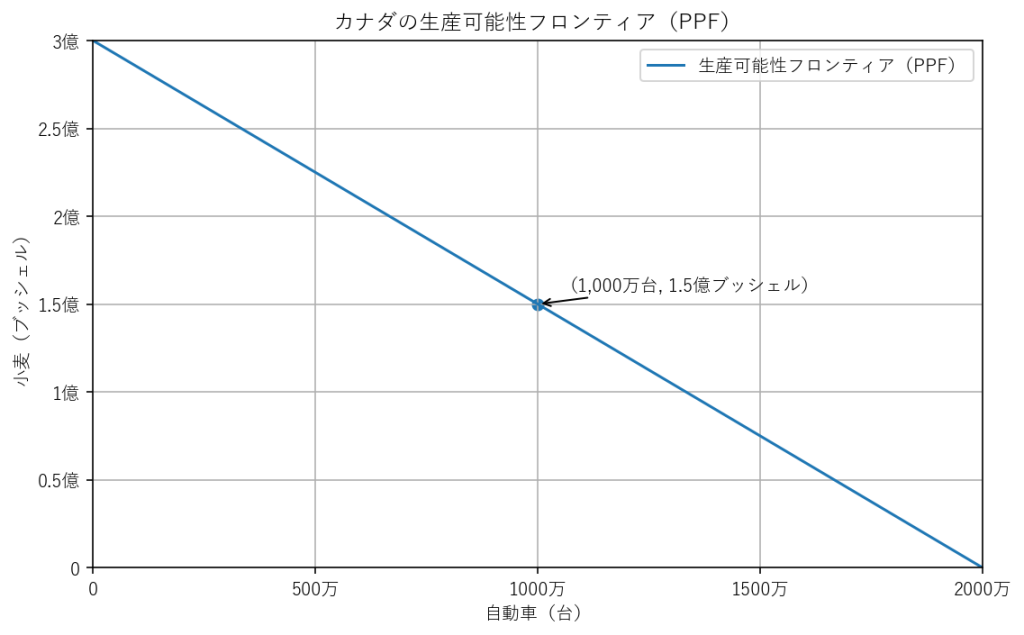
b. カナダの生産可能性フロンティア(PPF)と、車1,000万台を消費したいときの小麦
労働者は1,000万人なので、最大生産は次のとおりである。
- 自動車:\((10{,}000{,}000 \times 2 = 20{,}000{,}000)\) 台(2,000万台)である。
- 小麦:\((10{,}000{,}000 \times 30 = 300{,}000{,}000)\) ブッシェル(3億ブッシェル)である。
よってPPFは、点
- \((\text{自動車}0,\ \text{小麦}3億)\) と \((\text{自動車}2{,}000万,\ \text{小麦}0)\)
を結ぶ直線である。
PPFの式(小麦を縦、自動車を横)である。
\[
W = 300{,}000{,}000 – 15C
\]
(\(C\)=自動車台数、\(W\)=小麦ブッシェル)である。
貿易なしで自動車1,000万台を消費したいなら、生産も1,000万台である。
\[
W = 300{,}000{,}000 – 15 \times 10{,}000{,}000 = 150{,}000{,}000
\]
→ 小麦は1億5,000万ブッシェル消費可能である。
PPF上の対応点は (自動車1,000万台,小麦1億5,000万ブッシェル) である。
(図のイメージ)
- 横軸:自動車(0 → 2,000万)である。
- 縦軸:小麦(3億 → 0)である。
- その直線上の中点寄りに (1,000万, 1.5億) があるのである。
c. 取引提案(車1台=小麦20ブッシェルで、米国が車1,000万台購入)
米国が1,000万台買う=カナダは1,000万台輸出である。
カナダが引き続き国内で1,000万台消費するには、次が必要である。
- 生産は国内分1,000万+輸出分1,000万=合計2,000万台必要である。
- 2,000万台はカナダの最大生産なので、小麦は0ブッシェル生産である。
PPF上の生産点は (自動車2,000万台,小麦0) である。
輸出の見返りとして受け取る小麦は次である。
\[
20\ \text{ブッシェル/台} \times 10{,}000{,}000\ \text{台} = 200{,}000{,}000
\]
→ 2億ブッシェルである。
したがって、この取引後にカナダが消費できるのは次である。
- 自動車:国内消費分 1,000万台である。
- 小麦:受け取った 2億ブッシェルである。
貿易なし(b)では (1,000万台, 1.5億ブッシェル)だったので、同じ自動車1,000万台でも小麦が +5,000万ブッシェル増えるのである。
カナダは取引を受け入れるべきか?
受け入れるべきである。理由は次のとおりである。
- カナダの自動車1台の国内機会費用は 小麦15ブッシェルである。
- しかし取引では自動車1台あたり 小麦20ブッシェルもらえる(国内より有利)のである。
つまり、車を作って輸出したほうが、国内で同じ資源を使うより多くの小麦を得られ、消費可能集合がPPFの外へ広がるからである。