2章 – 演習と応用 4

a．各配分での生産量（1日あたり）

各人は10時間働くので、各人の最大生産は次のとおりである。

• ラリー：芝刈り10区画 または 洗車10台
• モー：芝刈り10区画 または 洗車20台
• カーリー：芝刈り20区画 または 洗車10台

これより、

（A）3人全員が芝刈りに全時間である。

• 芝刈り：10 + 10 + 20 = 40区画
• 洗車：0台

（B）3人全員が洗車に全時間である。

• 芝刈り：0区画
• 洗車：10 + 20 + 10 = 40台

（C）3人全員が半分ずつ（芝5時間・洗車5時間）である。

• ラリー：芝5区画、洗車5台
• モー：芝5区画、洗車10台
• カーリー：芝10区画、洗車5台

合計である。

• 芝刈り：5 + 5 + 10 = 20区画
• 洗車：5 + 10 + 5 = 20台

（D）ラリー半分ずつ、モーは洗車のみ、カーリーは芝刈りのみである。

• ラリー：芝5区画、洗車5台
• モー：洗車20台
• カーリー：芝20区画

合計である。

• 芝刈り：5 + 0 + 20 = 25区画
• 洗車：5 + 20 + 0 = 25台

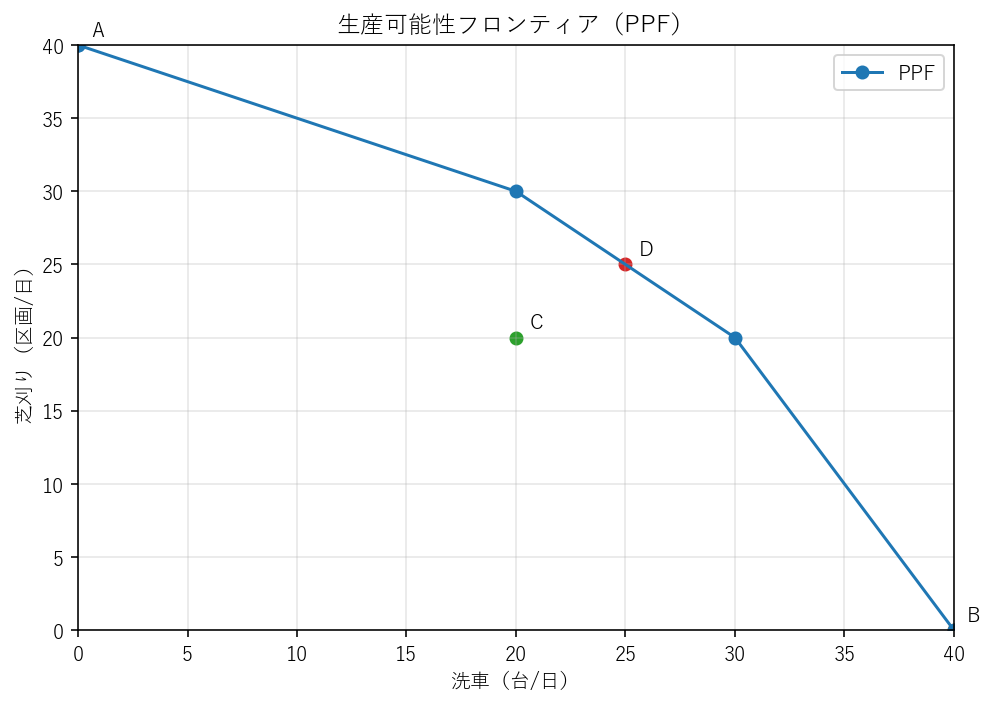
b．生産可能性フロンティア（PPF）の図示と A,B,C,D の位置

横軸を「洗車（台/日）」、縦軸を「芝刈り（区画/日）」とする。

比較優位（機会費用）を見ると、洗車の機会費用（芝刈りで支払うコスト）は次のとおりである。

• モー：洗車1台あたり芝0.5区画（最も安い）
• ラリー：洗車1台あたり芝1区画
• カーリー：洗車1台あたり芝2区画（最も高い）

よって、洗車を増やすときは モー→ラリー→カーリー の順に芝刈りから洗車へ回すのが効率的である。

その結果、PPFの折れ点（頂点）は次になるのである。

• 全員芝刈り：(洗車0, 芝40)
• モーを全て洗車へ：(洗車20, 芝30)
• 次にラリーを全て洗車へ：(洗車30, 芝20)
• 全員洗車：(洗車40, 芝0)

各点は次に位置するのである。

• A = (0,40)
• B = (40,0)
• C = (20,20)（PPFの内側）
• D = (25,25)（PPF上。ちょうど第2区間上）

c．PPFがそのような形をしている理由

PPFが原点に対して「外側にふくらむ（限界代替率が逓増する）」形になるのは、労働者ごとに比較優位（＝機会費用）が異なるからである。洗車を増やす初期段階では、洗車の機会費用が最も低いモーから芝刈り時間を洗車へ回すため、芝刈りの減少は小さい。しかし洗車をさらに増やすと、次にラリー、最後に機会費用が最も高いカーリーまで洗車へ回す必要が生じ、洗車を1台増やすために失う芝刈りが大きくなる。よって、PPFの傾き（芝刈り/洗車の犠牲）が次第に急になる形となるのである。

また本問は労働者が3人しかいないため、滑らかな曲線ではなく、労働者の切替点で折れ曲がる折れ線になるのである。

d．非効率な配分の有無

非効率な配分は C である。Cは (洗車20, 芝20) だが、洗車20台を保ったまま芝刈りを30区画まで増やせる。例えば、モーを洗車10時間（20台）に専念させ、ラリーとカーリーを芝刈り10時間ずつにすれば (洗車20, 芝30) を達成でき、Cを厳密に改善できる。よってCはPPFの内側にあり非効率である。

一方で AとBは端点としてPPF上にあり効率的であり、DもPPF上（(25,25)）にあるため効率的である。